La utilización de modelos matemáticos para comparar escenarios de propagación viral ha ganado popularidad en la pandemia de COVID-19. Para su correcta interpretación resulta imprescindible comprender sus alcances, limitaciones y supuestos. En esta nota se evalúan los peligros que conlleva la asunción de ciertos supuestos y se elucidan las ventajas de tomar en consideración la heterogeneidad demográfica, social y económica en el modelo epidemiológico. La necesidad de un enfoque interdisciplinario para la producción e interpretación de los resultados queda evidenciada y resulta central para asistir a la toma de decisiones, sobre todo en estos tiempos difíciles.

Sobre los modelos

Es de común acuerdo que se espera un progresivo aumento en el número de casos de COVID-19 en nuestro país en un futuro cercano. Muchas de las proyecciones realizadas con el fin de estimar el número de casos esperados están basadas en la aplicación de modelos matemáticos. La credibilidad de los mismos depende de la selección de distintos parámetros relacionados con las características del virus, muchas de las cuales no son conocidas con certeza al día de la fecha. Esto refleja la poca información que tenemos acerca del virus SARS-CoV-2 productor de la enfermedad COVID-19. La eficacia de estos modelos matemáticos para realizar predicciones reside en dos aspectos: por un lado acotarse a un problema particular donde el comportamiento del objeto de estudio sea, al menos parcialmente, conocido; por otro se busca simplificar la realidad basándose en lo que se conoce como “supuestos del modelo”. Este último aspecto es muy sensible, dado que de obviarse, puede tener fuertes implicancias en la interpretación de los resultados.

Aplicando el esquema del modelo SEIR

Uno de los modelos frecuentemente utilizados es el conocido como SEIR (Susceptible – Expuesto – Infectado – Recuperado) cuyo comportamiento se esquematiza en la Figura 1. El mismo asume que los individuos susceptibles, que son todos aquellos que no poseen inmunidad, una vez contagiados entran en un primer estado asintomático. Luego se pasa a un cuadro leve donde se presentan síntomas como fiebre, tos y/o dificultad respiratoria. La hospitalización no es un requisito esencial en esta etapa. Posteriormente se avanza a un cuadro severo en el cual se presenta un aumento de la frecuencia respiratoria y una baja en la saturación del oxígeno en sangre, en estos casos la hospitalización si es un requisito. El último cuadro es el crítico, en el cual se presentan fallas respiratorios graves, shock séptico y múltiples fallas orgánicas. En este último se requiere tratamiento en unidades de cuidado intensivos (UTI) y ventilación mecánica. En cualquiera de los estadios los individuos pueden recuperarse o bien progresar en la enfermedad hasta la muerte.

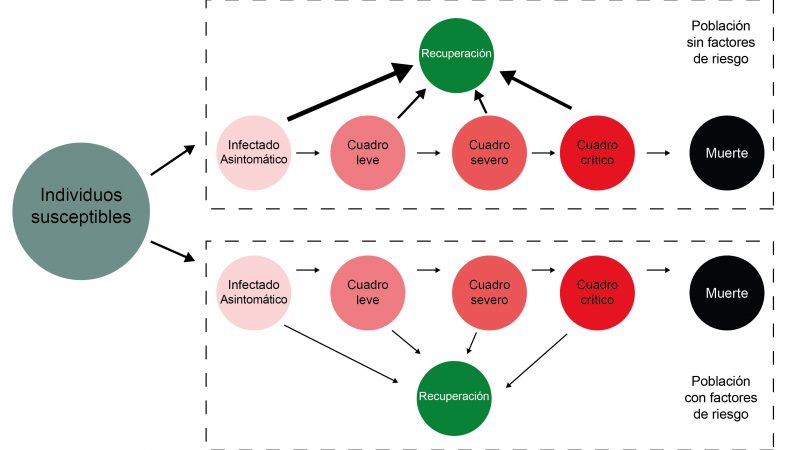
Definiendo los parámetros

Observando el esquema de la Figura 1 nos podríamos preguntar ¿Cuánto tarda una persona en pasar de un estado asintomático a presentar un cuadro leve? ¿Cuál es la probabilidad que tiene de recuperarse una persona en estado crítico? ¿Cuál es la probabilidad de que una persona que contraiga la enfermedad muera a causa de la misma? A estos tiempos y probabilidades que responden a las preguntas los llamamos parámetros y debemos ser muy cuidadosos al seleccionarlos. Estos parámetros le dan “vida” al modelo y permiten simular escenarios con condiciones que los afecten. Por ejemplo, se puede intentar comparar su comportamiento ante diferentes medidas que reduzcan la posibilidad de contagio.

El contexto de catástrofe dista del ensayo experimental ideal que nos permitiría conocer con rigurosidad las propiedades del virus.

Ahora bien, ¿dónde pueden obtener estos parámetros dado que muchos de ellos dependen de las propiedades del virus, el cual conocemos muy poco? Estos se pueden estudiar de experiencias que hayan tenido otros países con el virus pero, teniendo en cuenta el contexto dramático que conlleva la propagación de COVID-19, mucha de la información no se ha sistematizado o se hizo con distintos criterios en distintos países. El contexto de catástrofe dista del ensayo experimental ideal que nos permitiría conocer con rigurosidad las propiedades del virus.

En esta compleja situación un evento casual llamó la atención de muchos investigadores a nivel mundial: la propagación del COVID-19 entre pasajeros y tripulantes del crucero Diamond Princess, la cual se asemejaba a un buen experimento epidemiológico. Al arribar a la ciudad de Hong Kong uno de los tripulantes dió positivo en un testeo. Eso determinó que el barco fuera puesto en cuarentena y que aquellas personas del total de 3700 que había a bordo que presentaran síntomas fueran aisladas. Una vez levantada la medida, los pasajeros pudieron desembarcar y se supo que 619 individuos se habían contagiado. Este suceso permitió comprender la alta capacidad de propagación del virus, observar los síntomas que generó en distintos grupos etarios y en individuos con distintos antecedentes clínicos. Además, se estima que de no haber sido aislados dentro del crucero aquellos individuos con síntomas, la cantidad de infectados habría ascendido a 2300.

Con el paso del tiempo y la organización de la información de la experiencia de otros países se comenzó a conocer, en algunos aspectos, el comportamiento del virus y a darle valores a los parámetros. Algunos de estos son:

• Tipos de cuadros clínicos producidos por la infección: cerca del 80% de los casos reportados en China tuvieron un cuadro leve presentando síntomas como fiebre y dolor de garganta o dificultades respiratorias. El 14% desarrollaron un cuadro severo, que implica una neumonía que requiere hospitalización. El 6% derivó en un cuadro crítico necesitando cuidados intensivos.
• El período de incubación del virus: es el tiempo que se da entre que una una persona se contagia con el virus hasta que comienza a desarrollar síntomas. Dura alrededor de 5 días pudiéndose extender hasta más de 10.
• La tasa de letalidad: es el porcentaje de infectados que fallecieron por contraer la enfermedad y fue de 2,3% en China y 0,5% en Corea. Hay que tener en consideración que para los mayores de 80 años el porcentaje fue mayor (más del 10% en ambos casos).
• El número reproductivo básico (R0): indica la velocidad de propagación de la enfermedad y se encuentra entre 2 y 3 basándonos en el modelo chino y en el del crucero Diamond Princess.

Supuestos silenciosos que llevan a errores de interpretación

Ahora bien, el modelo no contempla ciertas posibilidades como por ejemplo que una persona pase de un cuadro severo a uno leve (como se vé en la Figura 1, las flechas van siempre en una sola dirección). Esto podría tener consecuencias en el cálculo de infectados pero asumimos que, si el impacto no es muy grande, lo podemos obviar con el fin de hacer más sencillos los cálculos. A este tipo decisiones que se toman y que permiten simplificar los cálculos se las conoce como “supuestos” del modelo. Muchos de los modelos discutidos e implementados con el fin de estudiar y predecir el comportamiento de la propagación de COVID-19 frente a la aplicación de diferentes medidas poseen dos supuestos que requieren atención especial:

• La probabilidad de contagiarse es igual para todos los individuos.
• La probabilidad de morir a causa de la infección es igual para todos los individuos.

Respecto al supuesto 1: la propagación del virus requiere el contacto cercano entre las personas, por lo tanto, es intuitivo pensar que ésta será menor en lugares con muy baja densidad poblacional. Este supuesto no es un grave problema para grandes ciudades, donde se puede asumir una distribución medianamente homogénea, pero sí lo es para gran parte de nuestro país donde existen regiones con alta concentración poblacional y otras con una muy baja cantidad de habitantes.

Si un modelo no tuviese en cuenta estos puntos no sería capaz de distinguir entre zonas que presentan mayores vulnerabilidades que otras.

Respecto al supuesto 2: se conoce que la probabilidad de morir por la enfermedad de COVID-19 guarda una relación con la edad y la presencia de enfermedades previas.

Si un modelo no tuviese en cuenta estos puntos no sería capaz de distinguir entre zonas que presentan mayores vulnerabilidades que otras.

Sin duda, aquellos lugares que tienen una población envejecida y/o con enfermedades previas que puedan potenciar la letalidad de COVID-19 deben ser priorizadas en la asignación de recursos.

Darle marcha al modelo

Con los parámetros seleccionados y teniendo en cuenta los supuestos ya podemos estar en condiciones de darle arranque a la simulación. A modo de ejemplo tomamos una región con 13.500.000 habitantes con una cantidad inicial de 200 personas infectadas (comienzan todas a la par, en estado asintomático) poniendo como fecha de inicio el 1 de abril. La simulación computacional comenzará a darle movimiento al modelo, esos 200 individuos contagiaran a otros y progresarán en los distintos estadíos de la enfermedad, o bien se recuperarán con los tiempos y las probabilidades establecidas por los parámetros. Esto nos dará un valor de infectados en cada estadio (asintomático, leve, severo o crítico) y la cantidad de muertos e individuos que se recuperaron para cada día.

El efecto de las medidas de distanciamiento tiene impacto directo sobre la velocidad de propagación (parámetro presente en el modelo) y se ha estudiado en distintos ejemplos a nivel mundial cómo diferentes medidas contribuyen a disminuir dicha velocidad.

Así mismo, se pueden plantear distintos escenarios de mitigación. Con el fin de comparar escenarios podemos proponer dos situaciones: en una, llamémosla A, luego de una cuarentena total de un mes, se permite libre circulación de la población en la región. En otra, llamémosla B, se continúa con medidas de mitigación sostenidas por más de tres meses. Esto implica evitar eventos que aglutinan a la población, controlar medios de transporte, preparar turnos diferenciales de trabajo, etc. El efecto de estas medidas tiene impacto directo sobre la velocidad de propagación (parámetro presente en el modelo) y se ha estudiado en distintos ejemplos a nivel mundial cómo diferentes medidas contribuyen a disminuir dicha velocidad.

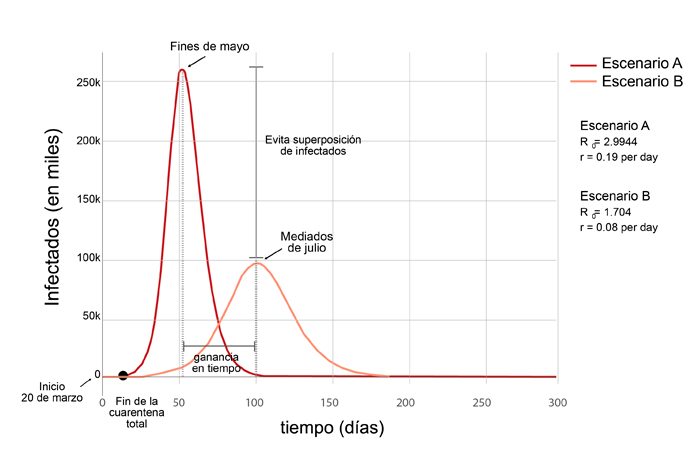
En la Figura 2 puede observarse la cantidad de infectados en estado severo y crítico (ambos grupos que requieren hospitalización) en función del tiempo. Una liberación de la circulación (escenario A) es seguida de un fuerte incremento de casos llegando a un pico a fines del mes de mayo. En cambio, manteniendo medidas de mitigación el pico se retrasa hasta mediados de julio y al achatarse se pasa de un escenario con un pico de 250 mil casos (escenario A) a uno de 100 mil casos (escenario B). Es importante destacar que, de todos modos, en ambos escenarios la cantidad de infectados que requieren hospitalización está muy por encima de las capacidades del sistema sanitario.

La importancia de un modelo que contemple características sociales, económicas y demográficas

Al plantear el modelo anterior se tomó en consideración la aplicación de una medida uniforme sobre toda la región. Sin embargo, existen dos supuestos importantes: por un lado la probabilidad de contagio es igual entre todos los habitantes, y por otro, la probabilidad de morir a causa de la enfermedad también.

Supongamos que, en base a un estudio que tiene en cuenta las características demográficas, sociales y económicas, logramos subdividir a la región planteada en el ejemplo de la Figura 2. Por un lado tenemos la subregión 1 que se la puede describir como una zona residencial que posee una densidad y tamaño poblacional bajos, con un porcentaje del 10% de población por encima de los 60 años. Esta presenta una gran cantidad de casos al inicio de la simulación (100 de los 200 casos). Como puede observarse, si se aplica el escenario B, el aumento paulatino de casos presenta una ventaja dado que al ser una zona residencial la posibilidad de un aislamiento domiciliario es factible y el número de casos que requieren hospitalización (suponemos un porcentaje más alto considerando una proporción superior a la media de adultos mayores a 60 años) puede ser controlable.

Por otro lado tomamos otra zona, que llamaremos subregión 2 (Figura 4) donde se registra un mayor nivel de hacinamiento y una cantidad de habitantes alta (1.500.000 habitantes), por lo tanto, se supone más velocidad de propagación viral lo que deriva en un gran número de casos. Es importante destacar que esta región posee muy pocos casos en el principio de la simulación y se considera una tasa de importación de infectados desde la región 1 (supongamos que podría ser por tránsito de personas entre ambas). En este caso una de las medidas del escenario B resulta muy efectiva, en la que puntualmente se considera evitar al máximo posible el contacto con la región 1, además de las otras medidas antes mencionadas.

Esto último es importante dado que significa más tiempo de reacción para detectar incrementos fuertes en la cantidad de casos mediante un monitoreo epidemiológico exhaustivo y localizado con el fin de aplicar medidas de mitigación más estrictas y/o dotar al sistema sanitario de recursos anticipándose al aumento de casos.

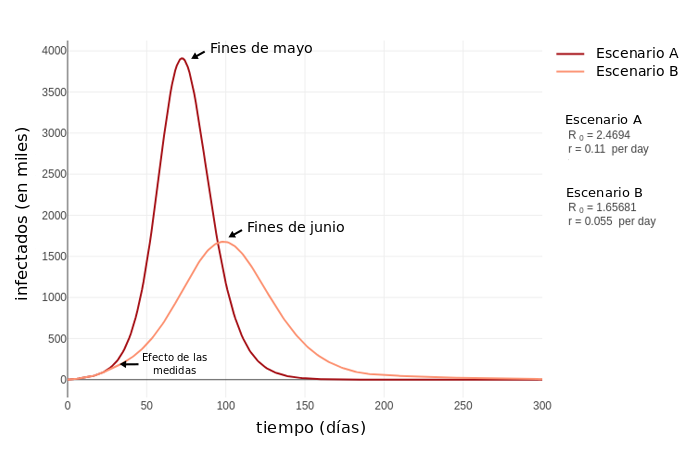
Analizando cada subregión por separado observamos distintas respuestas que pueden conllevar a diferentes tomas de decisiones. Mientras que en la subregión 1 bastaría con la aplicación de las medidas del escenario B, en la subregión 2 se debe continuar con un monitoreo exhaustivo con el fin de detectar posibles focos y tomar medidas que pueden incluir retomar la cuarentena social y obligatoria.

Para la correcta interpretación de los modelos es necesario adentrarse en los pilares que sostienen a dichos números, y estos son los parámetros y los supuestos del modelo.

Es importante también tener en cuenta el cuidado que se debería realizar sobre la subregión 2 con el fin de evitar la importación de casos, lo cual podría hacerse disminuyendo (o evitando) el tránsito entre estas subregiones.

Concluyendo

Sin entrar en formalismos matemáticos, es claro que la utilización de los modelos puede ser una herramienta útil para asistir a la toma de decisiones. Ahora bien, un peligro en el uso de los números como herramienta retórica es que, por sí mismos, no dicen nada. Para la correcta interpretación es necesario adentrarse en los pilares que sostienen a dichos números, y estos son los parámetros y los supuestos del modelo. Comprender esto resulta central para tomar dominio sobre los mismos y modificar los supuestos en función de los requerimientos que la problemática demanda. Al fin y al cabo todos los modelos están equivocados, pero algunos, son útiles.

· Franco Mársico ·

Biólogo. “Laboratorio de Redes Complejas, Instituto del Cálculo”, FCEN UBA. Asesor del Ministerio de Salud de la Provincia de Buenos Aires. Profesor Adjunto de la Universidad de José C Paz.